Angles Inscrits
I. Angle inscrit et Angle au centre associé
A. Rappels

Soit le cercle de centre O
-Une Corde est le segment liant deux points du cercle.
Exemple : [EF]
-Un diamètre est une corde passant par le centre du cercle. Exemple :[AB]
-Un rayon est tout segment liant le centre et un point du cercle. Exemple :[OC]
- L’arc de cercle est la portion du cercle comprise entre deux points du cercle.
Exemple : $\widehat{EF}$
B. Activité
Tracer un cercle (C) de centre O .
Soit A et B deux points distincts de (C ) . Placer un
point M sur le cercle distinct de A et de B et mesurer $\widehat{AMB}$ et $\widehat{AOB}$ dans les cas suivants :
a) $\widehat{AMB}$ est un angle aigu
b) $\widehat{AOB}$ est un angle obtus
Remarque


$\widehat{AMB}$ =38,66°Ì‚ $\widehat{AMB}$=111,3°
$\widehat{AOB}$=77,32° $\widehat{AOB}$ =222,61°
On remarque que dans tous les deux cas $\widehat{AOB}$ =2$\widehat{AMB}$
C. Définition
L’ angle $\widehat{AMB}$ est appelé angle INSCRIT dans le cercle ( C ). On dit qu’il intercepte
l’arc $\widehat{AB}$.
$\widehat{AOB}$ est un angle AU CENTRE ASSOCIE car il intercepte le même arc que
l'angle $\widehat{AMB}$ et son sommet O est le centre du cercle.
D. Théorème de l’angle inscrit
Soit un cercle de centre O. Si A ; B ; M sont trois points distincts de ce cercle , alors
$\widehat{AMB}$ = $\widehat{AOB}$
1. Exercice d’application
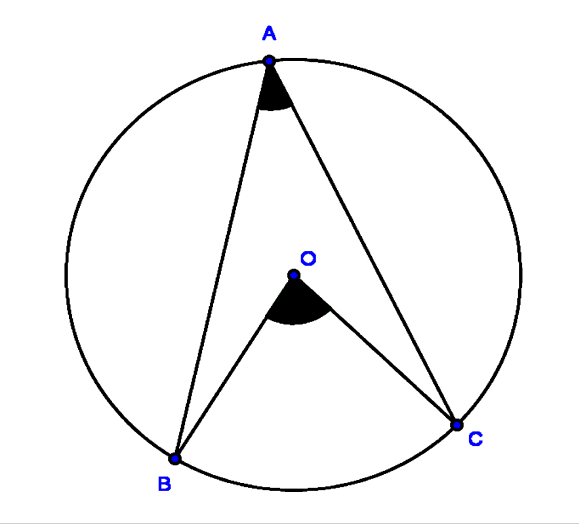
On donne le triangle ABC et son cercle circonscrit de centre O.
$\widehat{ABC}$=50° ; $\widehat{BCA}$Ì‚ = 70° .
Calculer $\widehat{BOC}$
2. Application : Triangle inscrit dans un demi – cercle
a - Activité
Soit un cercle de centre O. [AB] de diamètre et M un point du cercle .
Démontrer que AMB est un triangle rectangle.
Réponse

$\widehat{AMB}$ est un angle inscrit interceptant l’arc AB et $\widehat{AOB}$Ì‚ est un angle au centre associé interceptant le même arc AB , on a :
$\widehat{AOB}$Ì‚ = 2 $\widehat{AMB}$ ; $\widehat{AMB}$ =$\frac{\widehat{AOB}}{2}$ ; $\widehat{AMB}$ =$\frac{180}{2}$ =90o
Alos le trangle AMB est rectangle en M.
b - Propriété
Si un triangle AMB est inscrit dans un demi-cercle de diamètre [AB] alors AMB est un triangle rectangle M.
II. Angles inscrits interceptant le même arc
A. Activité
Tracer un cercle de centre O ,placer deux points distinct A et B sur ce cercle . Placer les points E ; F et M sur le grand arc AB et mesurer les angles $\widehat{AEB}$; $\widehat{AFB}$ et $\widehat{AMB}$. Que remarque t-on ?
Reponse
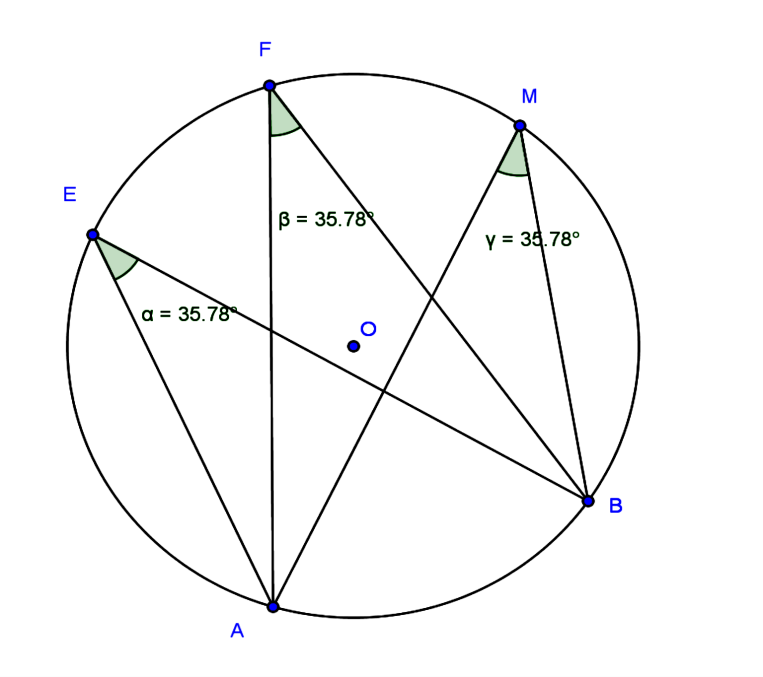
$\widehat{AEB}$ = 35,78° ; $\widehat{AFB}$= 35,78° et $\widehat{AMB}$ =35,78°.
On remarque que $\widehat{AEB}$; $\widehat{AFB}$ et $\widehat{AMB}$ sont des angles inscrits interceptant le même arc et qu’ils sont égaux.
B. Propriété
Si deux angles inscrits interceptent le même arc alors ils sont égaux.