Relations ; Fonctions
I. Notion de relation et de fonction
A. Exemple
Soit $A$ l’ensemble des pays suivants: $A= \{Burkina\ Faso, Mali, Tchad, Niger, Côte\ D’ivoire,Togo\}.$
Soit $B$ l’ensemble des villes suivantes : $B = \{Bamako, Bobo, Abidjan, Lagos, Lomé\}$
On décide d’associer un pays élément de $A$, à une ville élément de $B$, si cette ville est située dans ce pays par l’expression « est le pays où est situé »
La Côte D’ivoire est le pays où est situé Abidjan :
Le Burkina Faso est le pays où est situé Bobo
Le Togo est le pays où est situé Lomé
Le Mali est le pays où est situé Bamako
On remarque que les pays Tchad et Niger ne sont associés à aucun élément de $B$ et aucun élément de $A$ n’est associé à la ville Lagos.
On dit qu’on a une Relation de l’ensemble $A$ vers l’ensemble $B$.
L’expression « est le pays où est situé » est le lien verbal de cette relation.
Si nous remplaçons cette expression par R nous écrivons Mali R Bamako
Le couple ( Burkina, Bobo) ; correspond à une expression vraie
B. Notation – vocabulaire
La situation précédente fournit un exemple de Relation d’un ensemble A vers un ensemble B
L’ensemble A s’appelle l’ensemble de départ de la relation R
L’ensemble B s’appelle l’ensemble d’arrivée de la relation R
« Est le pays où est situé » est le lien verbal de la relation R
L’ensemble des couples qui permet d’obtenir toutes les phrases vraies est appelé graphe de la relation et est noté $G$.
$G=\{(Burkina,Bobo) ; (Mali,Bamoko) ; (Togo,Lomé) ; (Sénégal,Dakar)\}$
Bobo est l’ $image$ de Burkina, par cette relation. Burkina est l’ $antécédent$ de Bobo par cette relation
$ Couple = (antécédent, image) $
C. Définition
Une relation est définie par :
-un ensemble de départ
-un ensemble d’arrivée
-un ensemble de couple (ou lien verbal)
Une $fonction$ est une relation telle qu’à chaque élément de l’ensemble de départ correspond à au plus (ou aucun) un élément de l’ensemble d’arrivée.
II. Représentation d’une fonction
Il y’a plusieurs manières de représenter une fonction
A. Tableau de données
Considérons le tableau suivant donnant le relevé de la taille d’un garçon en fonction de son âge

B. Diagramme sagittal

On utilise cette représentation lorsqu’il y’a trop d’éléments dans l’ensemble de départ et
d’arrivée ou lorsque les éléments ne sont pas des nombres
C. Représentation graphique
1. Diagramme cartésien
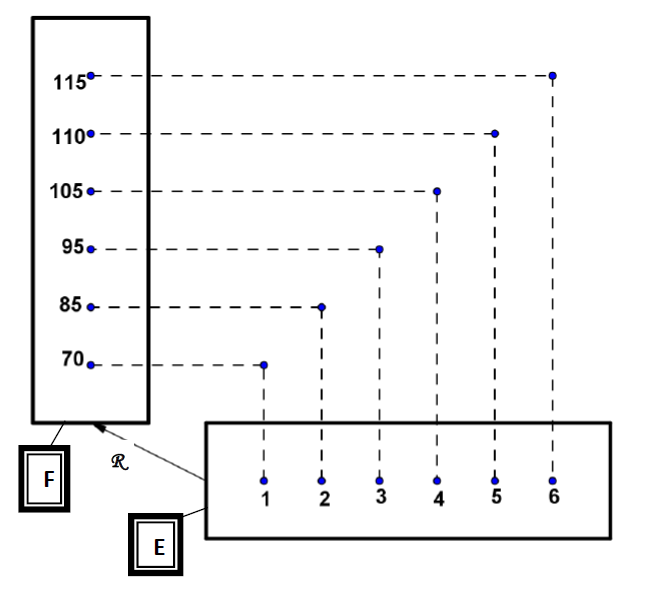
2. Diagramme en bâtons

Exercice d’application
Soit la représentation ci-dessous :

1)Quel est l’ensemble de départ et d’arrivée de cette relation ?
2)Quelle est l’image de d ?
3)Quel est l’antécédent de 5 ?
4)Cette relation est-elle une fonction ?
Corrigé
1) A est l’ensemble de départ de la relation et B est l’ensemble d’arrivée de la relation
2) 7 est l’image de d
3) e est l’antécédent de 5
4) Non, cette relation n’est pas une fonction car b a deux images