Proportionnalités
I. Suite proportionnelle
A. Activité
Le tableau suivant donne le prix des bâtons de craie en fonction du nombre de craie achetés
| N | 1 | 2 | 4 | 6 | 10 |
| P | 15 | 30 | 60 | 90 | 150 |
a) Comment calcule - t - on les prix des bâtons de craie à partir du nombre $(N)$ de bâtons de craie achetés?
b) Comment calcule - t - on le nombre de bâtons de craie achetés à partir du prix correspondant ?
Correction
a) Pour calculer le prix de bâtons de craie achetés on multiplie chaque fois par $15$ le nombre de bâtons de craie achetés.
b) Pour calculer le nombre de bâtons de craie achetés on divise le prix d’achat par $15$.
B. Vocabulaire
Chaque ligne du tableau représente une suite de nombres.
Exemple : $1, \,2, \,4, \,6, \,10$ est une suite de nombres.
Chaque nombre d’une suite est appelé terme de cette suite.
Exemple : $60$ est un terme.
C. Synthèse
On dit que les suites $N$ et $P$ sont proportionnelles.
$15$ est le $coefficient\:de\:proportionnalité$ faisant passer de la suite $N$ à la suite $P$.
D. Définition
Deux suites $N$ et $P$ sont proportionnelles si on peut obtenir les termes de la suite $P$ en multipliant les termes de la suite $N$ par un même nombre.
Ce Nombre est appelé le Coefficient de proportionnalité.
II. Calcul de la quatrième proportionnelle
A. Activité
Le tableau suivant nous donne le nombre $( J )$ des joueurs de football en $fonction$ des nombre $( E )$ d’équipes de football.
| E | 1 | 8 |
| J | 11 | n |
Calculer la valeur n sachant que nous sommes dans une solution de proportionalité
Correction
Calculons la valeur du nombre $n$
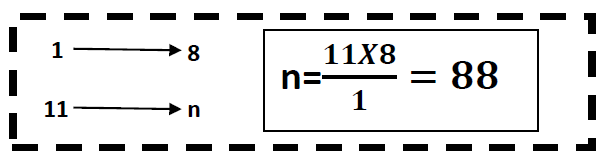
B. Retenons
Pour calculer le ou les termes marquant(s) de deux suites proportionnelles, on peut utiliser la règle de trois.
Exercice d’application
1) Trouver $b$ dans le tableau de proportionnalité
| 1 | 2 | 7 |
| 5 | 10 | b |
2) Le tableau suivant est il de proprtionnalité?
| X | 2 | 4 | 5 |
| Y | 6 | 12 | 15 |
Corrigé
1)Trouvons b dans le tableau de proportionnalité
$b = \frac{7 × 10}{2}$ = $35$
b = $35$
2)Le tableau est un tableau de proportionnalité
Réprésentation graphique
Reprenons l’exemple du tableau de I
| N | 1 | 2 | 4 | 6 | 10 |
| P | 15 | 30 | 60 | 90 | 150 |
On peut donner une représentation graphique de ce tableau.
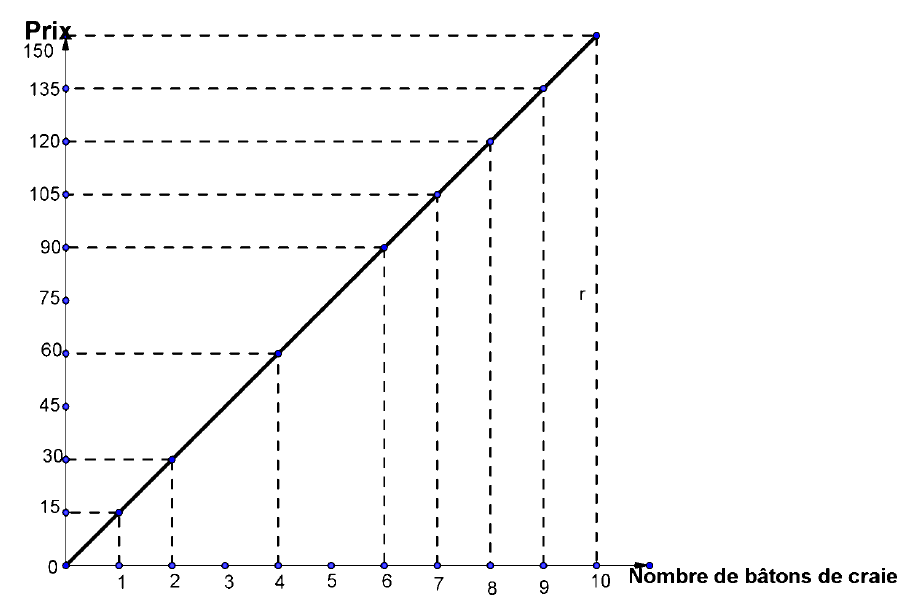
On remarque que les points de la représentation graphique sont alignés.
La représentation graphique de deux suites proportionnelles est formée de points alignés passant par l’origine du « repère »
III. Situation de proportionnalité
A. Distance parcourue-Durée du trajet
Le tableau ci-dessus indique la distance parcourue par une voiture en fonction du temps
| Distance en Km | 120 | 360 | 400 | 500 | 1440 |
| Durée en heure | 1 | 3 | 3,33 | 4,16 | 12 |
Ce tableau traduit une situation de proportionnalité car en multipliant par le même nombre $12$ la durée (en heure) on trouve la distance parcourue en ( $Km$).
$12$ est donc le $coefficient$ de proportionnalité faisant passer de la suite « Durée en heure » à la suite « Distance en $Km$ ».
B. Application d’un pourcentage
Le PDG d'une librairie fait $10\%$ de réduction sur le prix d’achat des différents documents( voir tableau ci-dessous)
| Documents | Maths 6è | Maths 3è | PC 4è |
| Prix en F CFA | 1800 | 2000 | 1500 |
| Rémise en F CFA | 180 | 200 | 150 |
Ce tableau traduit également une situation de proportionnalité. $\Large{\frac{10}{100}}$ est le coefficient de proportionnalité.