Théorème de Pythagore
I. Relations métriques dans un triangle rectangle
A. Activité
Construire un triangle $ABC$ rectangle en A. Construire l’hauteur $[AH]$.
1) Ecrire le rapport de projection orthogonale de la droite $(BA)$ sur $(BC)$.
2) Ecrire le rapport de projection orthogonale de la droite $(BC)$ sur $(BA)$.
3) Etablir une égalité entre les deux rapports de projection orthogonaux.
Réponse
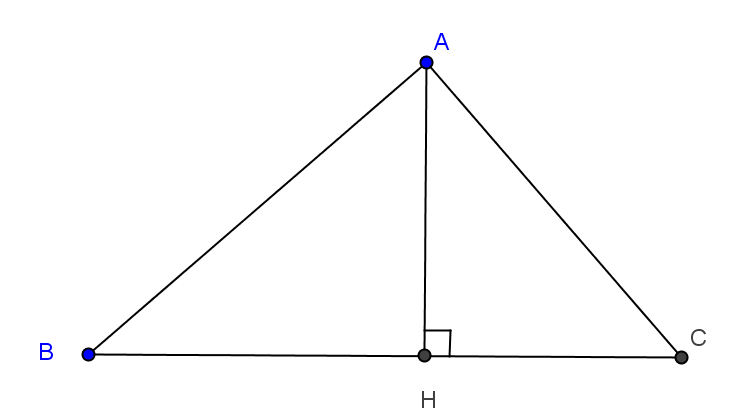
Soit P le projection orthogonal de $(BA)$ sur $(BC)$ et k son rapport.
On a : $P(B)=B ; P(A)= H$ alors k=$\frac{BH}{BA}$
Soit P’ le projection orthogonal de $(BC)$ sur $(BA)$ et k’ son rapport.
On a : $P(B)=B ; P(C)= A$ alors k’=$\frac{BA}{BC}$
Comme k=k’ on a $\frac{BH}{BA} \Longleftrightarrow BA^2= BH \times BC$
B. Première relation métrique dans le triangle rectangle
Etant donné un triangle $ABC$ de hauteur $[AH]$ , si $ABC$ est rectangle en $A$ alors : $BA^2= BH \times BC$
Remarque :
En utilisant le même triangle et en exprimant le rapport de projection de (CA) sur (CB) , de (CB) sur (CA) et sachant que les rapports k et k’ sont égaux on aura :
K=$\frac{CH}{CA}$ et k'=$\frac{CA}{CB}$
$\frac{CH}{CA}$= $\frac{CA}{CB}$ ⇔ $CA^2= CH × CB$
Exercice d ‘application
Soit ABC un triangle rectangle en A de hauteur [AH] tel que BC=8 et BH=2
Calculer $BA$ et $CA$ .
II. Théorème de Pythagore et sa réciproque
A. Théorème de Pythagore
1. Activité
Soit $ABC$ un triangle rectangle en $A$ de hauteur $[AH]$. A l‘aide des relations métriques dans le triangle rectangle $BA^2= BH \times BC$ et $CA^2=CH \times CB$ exprimer $BC$ en fonction de $CA$ et $BA$
Réponse
$BA^2= BH \times BC$
$CA^2 = CH \times CB$
En additionnant membre à membre on a:
$BA^2+CA^2 = BH \times BC + CH \times CB$
$BA^2+CA^2 = BC( BH + CH )$
$BA^2+CA^2 = BC \times BC$
$BA^2 + CA^2 = BC^2$
2. Théorème de Pythagore
Dans un triangle le carré de l’hypoténuse est égale à la somme des carrés des côtes perpendiculaires. Alors si ABC est un triangle rectangle en A on a :
$BC^2=AB^2+AC^2$
Exercice d’application
ABC est un triangle rectangle en A . Trouver la mesure du troisième côté dans les cas suivants :
- AC=5cm ; BA=3cm
- AB=4cm ; BC= 6cm
B. Réciproque du théorème de Pythagore
Si dans un triangle on a $BC^2=AB^2+AC^2$ alors ABC est un triangle rectangle en A
Exercice d’application
Soit un triangle ABC ; donner la nature de ce triangle dans les cas suivants :
- AB=5cm ; AC= 12cm ; BC=13Cm
- AB=7Cm ; AC=12Cm ; BC=$\sqrt{95}$
III. Autres relations métriques dans le triangle rectangle
A. Activité 1
Soit ABC un triangle rectangle en A et [AH] son hauteur.
a) Calculer la surface du triangle dans les deux représentations 1 et 2
b) Quelle relation peut –on déduire des deux calculs?
Reponse
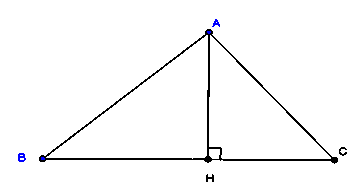
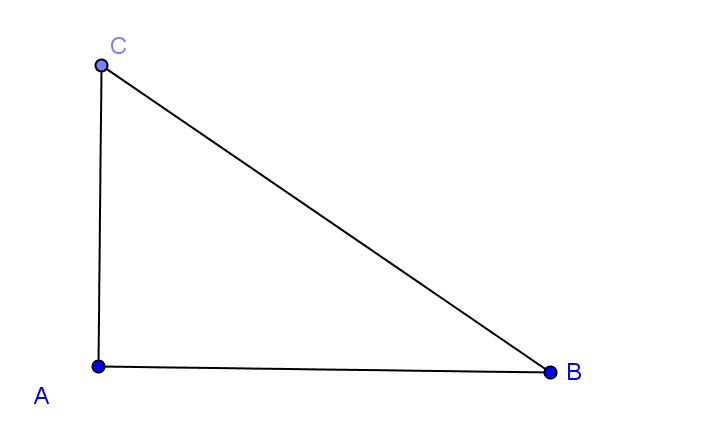
a) S1= $\frac{BC \times AH}{2}$ S2=$\frac{AC \times AB}{2}$
b) S1=S2 $\Longleftrightarrow \frac{BC \times AH}{2} =\frac{AC \times AB}{2} \Longleftrightarrow ( BC \times AH )=(AC \times AB)$
B. Activité 2
Soit $ABC$ un triangle rectangle en $A$ de hauteur $[AH]$ tel que $AB = 4$ ; $AC=4\sqrt{3}$ et $BC =8$.
a) Calculer $[AH]$ en utilisant la relation $BC \times AH= AC \times AB$.
b) Calculer $HB$ et $HC$ en considérant les triangle $BHA$ et $AHC$.
c) Calculer et comparer $AH^2$ et $HB \times HC$.
Réponse

a) calculons AH
$BC \times AH=AC \times AB $ $AH=\frac{AC \times AB}{BC}$ ; AH=$\frac{4\sqrt{3} \times 4}{8}$; AH=$2\sqrt{3}$.
b)Calculons HB et HC.
Considérons le triangle rectangle BHA :
$AH^2 +HB^2=AB^2$ ; $HB^2= AB^2- AH^2$ ; $HB^2=4^2 –(2\sqrt{3})$ ; $HB^2=16 -12$ ; $HB^2=4$ ; $HB=\sqrt{4}$ ;
Considérons le triangle rectangle CHA :
$AH^2 +HC^2=AC^2$ ; $HC^2= AC^2- AH^2$ ; $HC^2=(4\sqrt{3})^2 - (2\sqrt{3})^2$ ; $HC^2=36$ ; $HC= \sqrt{36}$ ; $HC=6$
c) calculons
$AH^2 =(2\sqrt{3})^2=4 \times 3=12$
$HB \times HC= 2 \times 6= 12$
Alors
$AH^2=HB \times HC$
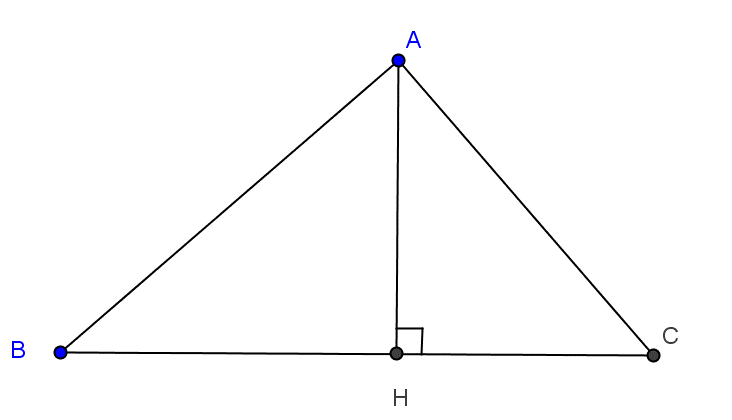
C. Relatons Métriques
Etant donné un triangle ABC de hauteur [AH], si ABC est rectangle en A alors:
$AC$ x $AB=BC$ x $AH$
$AH^2=HB$ x $HC$
IV. Application du théorème de Pythagore
A. Carré
ABCD est un carré de côté a . Déterminer la mesure de la diagonale d.
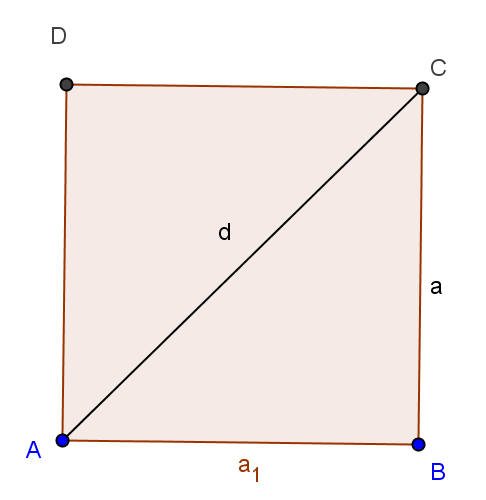
Considérons le triangle ABC rectangle en B
$AC^2= AB^2+BC^2;\; d^2 = a^2+ a^2;\; d^2= 2a^2;$
d=a$\sqrt{2}$
B. Triangle équilatéral
ABC est un triangle équilatéral de côté a . Déterminer la mesure de la hauteur h.

Considérons le triangle ACH
$\mathbf{AC^2=AH^2 + CH^2\;;\; a^2= (\frac{a}{2})^2+h^2 \;;\; h^2=a^2-\frac{a^2}{4} \;;\; h^2=\frac{3a^2}{4} \;;\; h=\sqrt{\frac{3a^2}{4}} \;;\; h=a\frac{\sqrt{3}}{2}}$
C. Distance d’un point à une droite
1. activité
Soit une droite (D) et M un point n’appartenant pas à (D) ; H est le projeté orthogonal de M sur (D).
Placer les points A ; B et C sur (D) et déterminer la plus petite distance de M à (D).
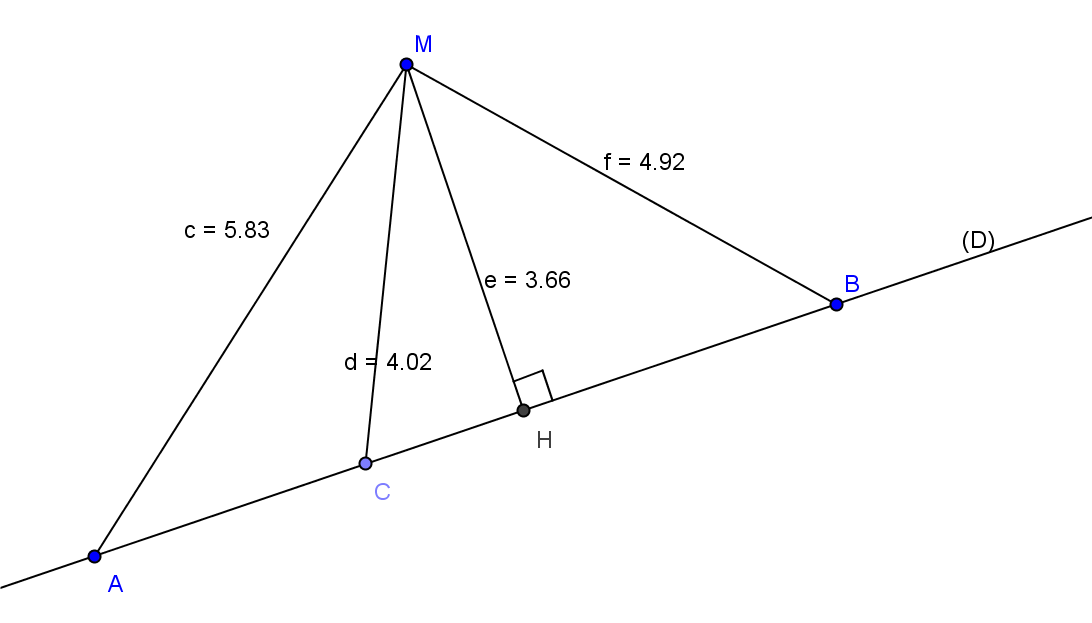
La distance MH est la plus courte distance de M à (D).
2. Définition
La distance d’un point M à une droite (D) est la plus courte des distances du point à la droite (D).
3. Propriété
La distance d’un point M à une droite (D) est la distance de ce point à son projeté orthogonal H sur (D).